|
Home » Sponsored » Pi Speakers » H290C Horn/Waveguide (Upgrade for the obsolete Eminence H290)
|
|
|
|
|
|
|
|
| Re: H290C Horn/Waveguide [message #76563 is a reply to message #76448] |
Tue, 30 April 2013 13:15   |
 |
Wayne Parham
Messages: 18786
Registered: January 2001
|
Illuminati (33rd Degree) |
|
|
In the chart above, you can only really see evidence of waistbanding in the 12dB strata. As I said, I think this is largely caused by the renderer, which seems to fill the strata with any values less than the stratification level without any interpolation or curve fiting. The waistbanding level is less than 6dB lower than midband, so it just doesn't show up.
Also, the scale is logarithmic which reduces the size of the waistbanding region, making it more difficult to see.
To help better illustrate waistbanding in the H290C, we can change the scale of the sonogram to logarithmic. That stretches the area where waistbanding occurs. See the charts below:
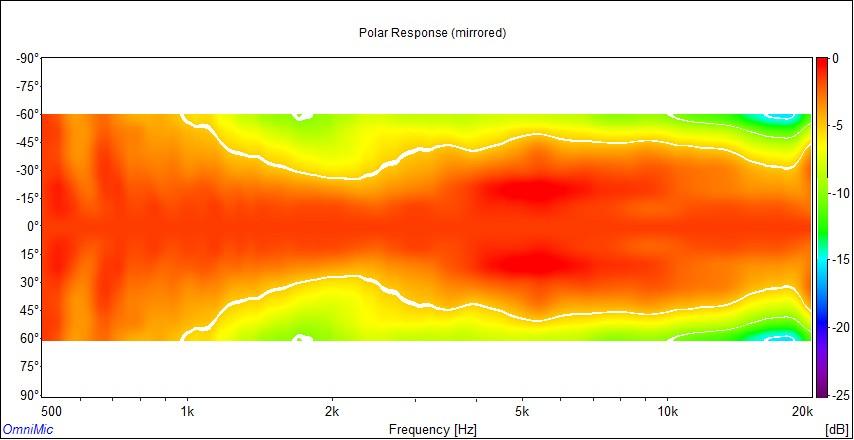H290C horizontal sonogram using logarithmic scale
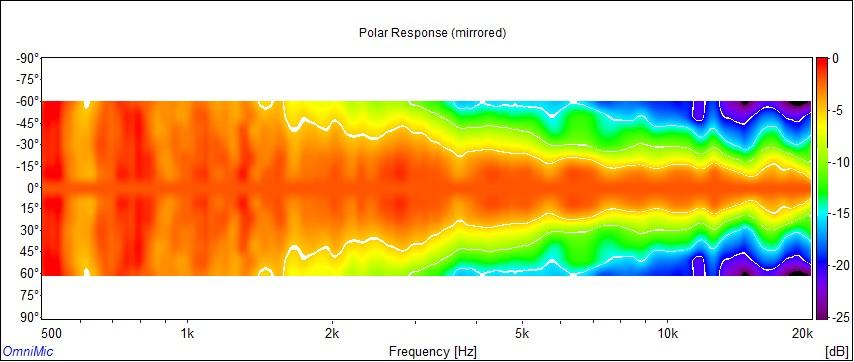H290C vertical sonogram using logarithmic scale
These are sonograms made for the H290C using a different renderer and plotted on a logarithmic scale. The measurements were made in a different environment too, so there are slight differences in the data but it shows general agreement with the other measurements. The biggest difference is in the rendering and the logarithmic scale, where here we can sort of put the waistbanding region under a magnifying glass.
See the color scale at the right side of each chart. This legend shows us a color gradient mapped to SPL.
You will notice that horizontal waistbanding centers around 1.8kHz, and its effects are about 2dB reduction of sound at 45° compared to the midband levels. That's what waistbanding does. It reduces output slightly at the edge of the beam.
As a sanity check, we can calculate waveguide beamwidth using formulas from Keele's paper, "What's so Sacred About Exponential Horns?"
Pattern Control Lower Limit = (106 / Mouth Width * Wall Angle)
Waistbanding Frequency = 1.5 * Pattern Control Lower Limit
Waistbanding Pinch Angle = 2 * Pattern Control Lower Limit / 3
Therefore, the H290C has properties somewhere in this range:
106 / 11" * 85° = 1070Hz (lower limit of pattern control)
1070 * 1.5 = 1.6kHz (waistbanding center frequency)
2 * 85 / 3 = 60° (waistbanding minimum beamwidth angle)
Earlier measurements showed waistbanding centered around 1.4kHz. The measurements above show it to be centered around 1.8kHz. Both are reasonable, given the different environments they were taken in, and both match our expectations of 1.6kHz fairly well. One is a little higher than predicted, the other a little lower, but both are within 10% of what Keele's formula predicts. In each case, you can look at the charts and see less output at the waistbanding minimum frequency than midband. It falls a couple decibels more in the waistbanding region than it does at higher frequencies.
In my opinion, the 2dB loss at 45° from waistbanding is acceptable, especially since the woofer and tweeter are blended in the crossover region anyway. Even if they weren't, as is increasingly the case with the larger midwoofers, what we're really talking about here is a slight decrease in output at wide off-axis angles. By slight, I mean practically nothing. The 2dB drop at wide off-axis angles is completely inaudible.
Waistbanding is more damaging in a prosound implementation. In that application, the problem is not so much the slight squeeze of the pattern as it is the secondary lobe, which affects arrayability. But in this case, we're not concerned with that. A two-way or three-way speaker using an H290C waveguide has no other sources with radiation at angles that would create an interference pattern with the secondary lobe.
The thrust of the H290C design approach was to shift all anomalous behavior as low in frequency as possible. The idea was to sacrifice a little bit of waistbanding at the bottom end for smoothness from midband up. Crossover occurs between 1.2kHz and 1.8kHz, with that region blending woofer and tweeter output together. So by optimizing tweeter performance above that point, we are optimizing where tweeter fidelity is needed the most.
What we gain in the trade is a flare profile that keeps the wavefront propogation perfectly perpendicular to the wall angle all the way through the horn. We also gain better acoustic loading, which is important in a conical horn or waveguide, because they are characteristically weak in this regard. They need all the help they can get. Improved acoustic loading provides smoother response, greater efficiency and lower distortion.
We haven't talked much about distortion, but consider that for a moment. By increasing efficiency, you reduce drive requirements. So not only does the improved acoustic load reduce diaphragm excursion, but it also increases efficiency, which reduces the drive requirements as well. This, in turn, reduces excursion even further.
A 3dB increase in sensitivity means 1/2 power is required to obtain the same SPL. So the distortion reduction is improved by two mechanisms, one being the reduced excursion from loading, the other being reduced excursion from reduced drive signal. The improvements from horn loading are cumulative where distortion reduction is concerned. This is true in all horns, basshorns and midhorns, but even more true in compression drivers, because they are designed for use where loading is good. They do not have much excursion capability, because they're designed to be used on a horn, not on a baffle.
|
|
|
|
|
|
| Re: H290C Horn/Waveguide [message #78533 is a reply to message #77006] |
Tue, 03 December 2013 16:32 |
|
Wayne Parham
Messages: 18786
Registered: January 2001
|
Illuminati (33rd Degree) |
|
|
There were several influences that drove my decision to create this horn. The most important one was an observation that radial horns having relatively constant horizontal directivity sounded best to me. Objectively, they had smooth response and uniform horizontal directivity. Their physical features were much like modern waveguides, having no sharp edges in the flare.
The H290C is very much like a radial horn of similar size, except that its OSEC flare profile is defined as the hyperbola created from a line drawn tangent to an elliptic cylinder or oblate spheroid:
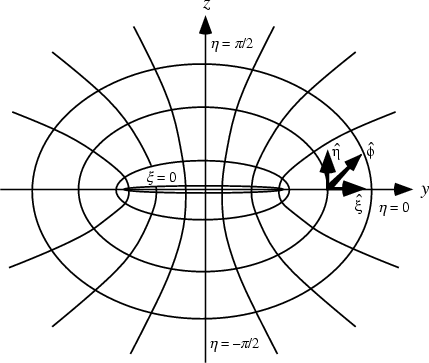
When I first heard about this flare profile, I began to study it and found this shape was used in other disciplines as an antenna, horn, lense or other waveform radiator. This is an important "litmus test" for me, because the most successful ideas tend to be used in all engineering fields. Where I see things in just one field (and especially in audio), I am skeptical. Audio is saturated with fads and misguided pseudo-science, some even coming from big names in the industry. But this isn't one of them, and devices created using this profile provide fairly clear advantages.
However, the advantages are only found if (and this is a big "if") the waveguide/horn is properly built. Just having this basic shape isn't enough. Just like you can make a good exponential horn or a bad one, or even more so a good conical horn or a bad one, this flare profile has a few "sweet spots" and a bunch that aren't so hot. One is well advised to model the horn, optimizing it for best response and beamwidth/coverage. It isn't a "given" that this particular profile can be used no matter what exit angle is desired. Some work well, but some, not so much.
That was the basis for the last post, just above. It gives a feel for a well designed horn, and one that isn't optimized as well. Both have the same coverage pattern, but one has significantly more ripple.
More information:
- The Sound Field and Radiation Impedance of a Hyperbolic Horn, by Vincent Salmon. This is the classic paper defining "Salmon family" horns.
- The Webster Equation Revisited, by Sjoerd Rienstra. Another look at the famous 1P model, and it's limitations.
- Reply to "How Horns Work", an overview on horns based on elliptical coordinate systems by Earl Geddes.
- The horn-feed problem: sound waves in a tube joined to a cone, and related problems, by P. A. Martin. This paper looks at the interface between planar source and waveguide, and it invites a study of other disciplines, such as waveguide/horns used for electromagnetic radiation.
- Geometrical representation of the fundamental mode of a Gaussian beam in oblate spheroidal coordinates, by Barbara Landesman. This paper looks at the fundamental propogation mode and higher-order modes when using devices based on oblate spheroidal coordinates.
- A New Mathematical Model for a Propagating Gaussian Beam, another look at wave propogation through OS devices by Barbara Landesman
- The Paraxial Approximation, an explanation of the concept.
- Optimum Horn Mouth Size, by Don Keele. A paper written that speculates there is an optimum horn mouth size. It suggests that the radiation is neither planar nor spherical, but something in between.
- Wave Propagation and Radiation in a Horn: Comparisons Between Models and Measurements, by Eveno, Dalmont, Caussé and Gilbert. Further study of the planar versus spherical radiaton models, a comparison showing differences.
- Input impedance computation for wind instruments based upon the Webster-Lokshin model with curvilinear abscissa, by Thomas Hélie, Thomas Hézard and Rémi Mignot. This paper models horns and waveguides using an improved 1P approach that accounts for visco-thermal losses at the horn walls.
- Computer Simulation of the Acoustic Impedance of Modern Orchestral Horns, by A. Benoit and J.P. Chick. A study of computer models used to calculate horn impedance. It proposes using a 3D element model rather than a 1P transmission line model for greater accuracy.
- A Modeling and Measurement Study of Acoustic Horns, by John Post and Elmer Hixson. An exhaustive study of models and measurements, and of comparisons between them, seeking to refine models. Both 1P and 3D approaches are explored. It discuses propogation modes in some detail, from primary to high-order modes. Appendix A discusses Electromagnetic and Acoustic analogies, which I think is always important. I personally look for things that span across multiple disciplines, because truly good approaches always do.
- Horn Loaded Loudspeakers, by Richard Morgans at the Department of Mechanical Engineering, University of Adelaide. This is another very elaborate study of various approaches to using mathematical models to simulate horns, and comparing them with actual measurements.
|
|
|
|
|
|
| Re: H290C Horn/Waveguide - closest equiv. in 1.5" or 2"? [message #92337 is a reply to message #92335] |
Thu, 17 September 2020 23:09 |
|
Wayne Parham
Messages: 18786
Registered: January 2001
|
Illuminati (33rd Degree) |
|
|
I put all of my focus on the H290C, and it's predecessor, the H390C. That was a wood horn/waveguide with the same profile but with much more mouth radius because it was designed to be free-standing and therefore have no baffle loading. But both are for 1" exit compression drivers.
I was able to do most of the acoustic development work back when I was making the H390C because it was cut on a CNC machine. So I was able to cut a physical model, test it and make incremental improvements.
Sometimes, lessons learned with one size driver don't transfer to another. But I find this more true of cone drivers than of compression drivers. So some of what I learned while optimizing the 1" drivers might transfer to larger drivers.
Here are a few main points:
1. The basic flare starts with an oblate spheroidal profile and then transitions to a flare based on elliptic cylindrical geometry. Said more simply, the throat is round and the mouth is rectangular. The same OS expansion equation is used to plot each axis, but the asymptotic angle is different in order to get the 90° x 40° shape.
A similar profile can be created with a OS to PS transition. That's oblate spheroidal to prolate spheroidal. It makes a very similar horn/waveguide but the mouth is oval-shaped instead of rectangular.
Each of these three coordinate systems are related: OS, PS and EC. They all make very similar flare profiles, just with different shaped mouths. Oblate spheroidal horn/waveguides are round, prolate spheroids are oval and elliptic cylinders are rectangular.
2. I find that acoustic loading is important. Waveguides are closely related to conical horns, which don't load well at low frequencies. But they still provide some acoustic loading and I think this is important to sound quality. So do not discount the quality of acoustic loading.
3. Radiusing the mouth edge, gradually opening up wider than the OS/EC profile, helps reduce waistbanding at the lower frequency range. With the right amount of radius area, you can completely eliminate waistbanding. But the radiused area does not contribute any acoustic loading. So it's almost like the horn/waveguide length ends at the point where the OS profile ends and the radiused profile begins.
4. Another thing that affects acoustic loading is the expansion rate. A horn/waveguide that has less expansion loads better. But this necessarily limits the overall coverage angle. I found empirically that a 90° x 40° waveguide is about as wide as can provide enough acoustic loading to offer smooth response. Any wider and the quarter-wave modes become pronounced, especially if a lot of the profile is sacrificed for waistband-reducing radius. For example, the H290C is actually a smidge under 90° in the horizontal, and it uses baffle loading rather than a lot of radiusing at the mouth.
5. If large size is not a problem, then you can have enough mouth radius to completely eliminate waistbanding and still have enough length to provide good acoustic loading. This makes a pretty large device though, and the extra mouth area prevents close vertical spacing between the waveguide and the adjacent driver in the system. This can make it hard to get the forward lobe tall enough - The vertical nulls might narrow too far. But with a low enough crossover point, the system can have wider vertical spacing between subsystems and still have a nice tall forward lobe with widely spaced vertical nulls.
|
|
|
|
|
|
Goto Forum:
Current Time: Mon Nov 25 10:06:40 CST 2024
|
Posting Rules
Members
Search
Help
Register
Login
Get a T-Shirt!
